Radiação do corpo negro FÍSICA
EXPLORAÇÃO DE SIMULAÇÕES COMPUTACIONAIS
Para utilizar a simulação é necessária a instalação prévia do software JAVA.
Caso o software não esteja instalado, ao aceder à simulação, automaticamente, é pedida a sua instalação.
[1] Simulação da autoria de St. Norbert College, Wisconsin, Estados Unidos da América, disponível em 18/02/2014
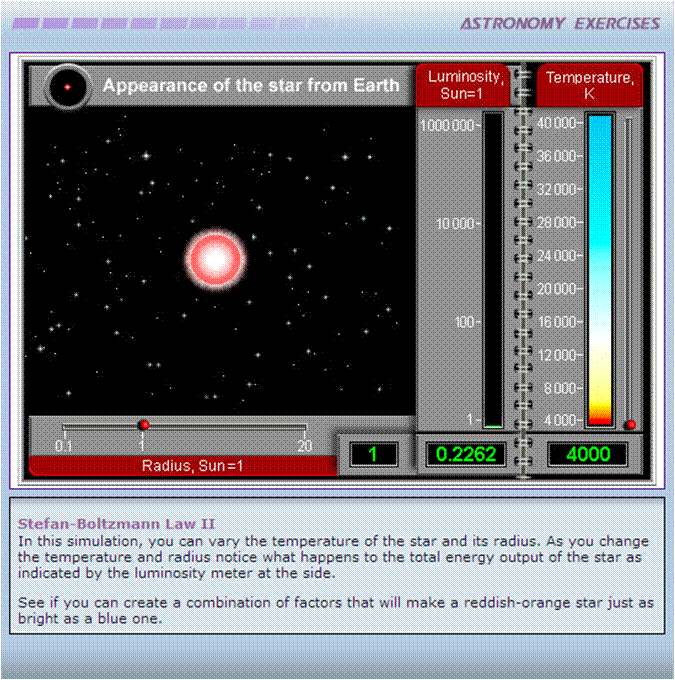
A simulação computacional permite-te definir a temperatura a que se encontra uma determinada estrela como também o seu raio, que altera a área de superfície emissora da estrela.
Para diferentes valores de temperatura e de raio da estrela podes observar a alteração de uma outra variável que se ajusta automaticamente. Essa variável é a luminosidade da estrela (“luminosity”) e aparece como uma grandeza relativa em função da luminosidade do Sol.
Fisicamente essa variável é designada por potência total da radiação emitida por um determinado corpo, sendo designada de luminosidade na Astronomia.
Matematicamente a variável relativa, luminosidade da estrela (ou potência total emitida por um corpo negro), pode ser descrita pela relação:
Onde L estrela é a luminosidade da estrela, L Sol é a luminosidade do Sol, P emitida pela estrela é a potência total de radiação emitida pela estrela, e P emitida pelo Sol é a potência total de radiação emitida pelo Sol.
Também o raio da estrela (“radius”) apresentado é uma medida relativa. É uma grandeza que apresenta o raio da estrela em função do raio do Sol. Tal como a luminosidade, esta grandeza pode ser descrita matematicamente pela relação:
Onde R estrela é o raio da estrela e R Sol é o raio do Sol.
Nota também que, ao contrário das simulações exploradas anteriormente sobre o estudo da lei de deslocamento de Wien, as cores das estrelas apresentadas são as cores vistas da Terra. Como o efeito da atmosfera na dispersão e absorção da radiação é significativo, as cores apresentadas são diferentes das cores das estrelas quando observadas do espaço.
Segue então a proposta de exploração apresentada que te irá ajudar na compreensão da Lei de Stefan-Boltzmann.
1 - Começa a exploração da simulação analisando-a atentamente.
-
Repara nos eixos das variáveis apresentadas e explica por que é que apenas a grandeza temperatura apresenta unidades.
2 - Mantendo o valor do raio da estrela fixo, varia a sua temperatura e observa a variação da luminosidade.
-
Que tipo de relação existe entre a temperatura da estrela e a sua luminosidade?
3 - Agora, mantém a temperatura da estrela num valor fixo, e varia o seu raio.
-
Observando de novo a variação da luminosidade da estrela, indica como varia esta grandeza em função do seu raio.
4 - Seguindo a sugestão feita na simulação, tenta combinar as variáveis possíveis de forma a obteres uma estrela vermelha/alaranjada tão brilhante como uma estrela azul.
-
Pensavas que uma estrela mais fria poderia ser tão brilhante como uma estrela mais quente? O que concluis acerca da luminosidade de uma estrela?
5 - Para uma análise mais quantitativa destas relações é necessário recorrer a um tratamento gráfico dos resultados observados.
Num primeiro passo vamos estudar a relação entre a área da superfície emissora de radiação do corpo e a sua luminosidade. Para isso, regista 10 pares de valores do raio relativo (distribuídos ao longo da escala do raio relativo) e da luminosidade da estrela para uma determinada temperatura que deve ser mantida fixa ao longo de todo este passo.
Regista esses valores numa tabela como a exemplificada:
-
Explica por que é que os valores do raio relativo da estrela a registar devem ser distribuídos ao longo da escala disponível.
6 - Usando o software Excel da Microsoft, copia a tabela com os valores registados para uma folha de cálculo do software.
7 - A relação que pretendemos determinar não é uma relação entre o raio da estrela e a sua luminosidade mas sim entre a área da superfície da estrela e a sua luminosidade. É necessário então calcular a área da superfície de uma estrela.
-
Apresenta a fórmula matemática que te permite calcular a área de uma superfície esférica a partir do raio dessa esfera.
-
Constrói uma nova coluna na tua tabela e calcula os valores das áreas de superfície relativas das estrelas com base no seu raio relativo.
8 - O método gráfico permite facilmente verificar a relação entre duas grandezas, bastando para isso encontrar uma relação linear entre essas mesmas variáveis. Constrói então um gráfico de dispersão colocando no eixo Y os valores da luminosidade relativa e no eixo X os valores das respetivas áreas de superfície relativas.
-
O que se pode afirmar acerca da relação existente entre as variáveis?
-
Verifica-se a existência de linearidade?
9 - No segundo momento desta exploração, vamos estudar a relação existente entre a luminosidade da estrela e a sua temperatura. Desta vez, regista 10 pares de valores de temperatura (também distribuídos ao longo da escala de temperaturas) e da luminosidade da estrela, mantendo a outra variável, o raio da estrela, constante. Regista também esses valores numa tabela como a seguinte:
-
Repara nas unidades de temperatura. É necessário convertê-las nas respetivas unidades S.I.?
-
Tal como os valores do raio relativo da estrela registados, também estes valores necessitam de ser distribuídos ao longo da escala de temperaturas?
10 - Copia a tabela com os teus registos para a folha de cálculo já utilizada.
11 - Para encontrar a relação que pretendemos determinar, podemos recorrer de novo ao método gráfico. Constrói um novo gráfico de dispersão onde no eixo Y estejam representados os valores da luminosidade relativa e no eixo X os valores das respetivas temperaturas das diferentes estrelas.
-
Observaste a linearidade pretendida?
12 - Constrói novas colunas na tua tabela onde calcules os valores da temperatura ao quadrado, ao cubo e elevada à quarta potência. Constrói três gráficos de dispersão onde, em cada um, representes:
No eixo Y os valores da luminosidade relativa e no eixo X os valores do quadrado das respetivas temperaturas.
No eixo Y os valores da luminosidade relativa e no eixo X os valores do cubo das respetivas temperaturas.
No eixo Y os valores da luminosidade relativa e no eixo X os valores da quarta potência das respetivas temperaturas.
-
Em algum dos casos encontraste uma relação de linearidade?
-
Que se pode afirmar acerca da relação da temperatura da estrela com a sua luminosidade?
13 - Da análise dos 2 momentos da exploração desta simulação, o que se pode concluir acerca da relação entre a luminosidade da estrela, a área da sua superfície e a sua temperatura?
14 - A lei que relaciona a potência total de radiação emitida por um corpo negro com a sua temperatura e com a área da sua superfície designa-se por Lei de Stefan-Boltzmann e foi enunciada pelos físicos Joseph Stefan e Ludwig Boltzmann em 1879 e 1884, respetivamente.
Para um corpo negro, como é o caso (em boa aproximação) das estrelas, existe uma constante de proporcionalidade que relaciona a potência total de radiação emitida por uma estrela com a área da sua superfície e uma potência da sua temperatura. Essa constante designa-se por constante de Stefan-Boltzmann, em homenagem aos cientistas que a descobriram, e representa-se pela letra σ, tendo valor :
-
Como sabes, a luminosidade tem o mesmo significado de potência total de radiação emitida. Com base nas relações encontradas entre a luminosidade e a área da superfície da estrela e a sua temperatura, formula matematicamente a Lei de Stefan-Boltzmann.
Lei de Stefan-Boltzmann
-
Exploração
Para explorares esta simulação[1] clica na imagem.
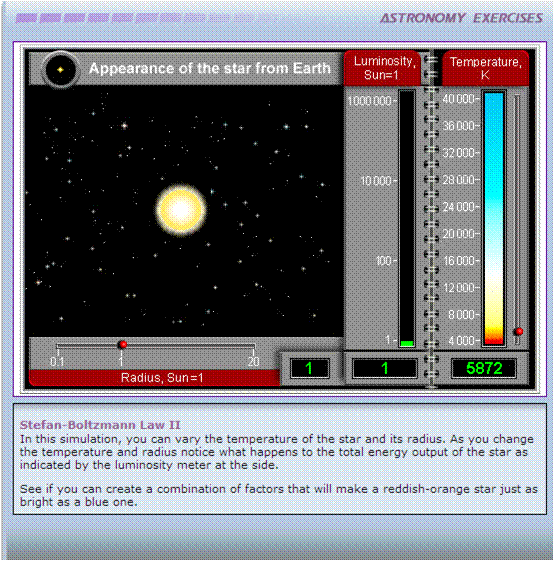
Luminosidade da estrela
Ajuste da temperatura
Ajuste do raio da estrela
Cor da estrela
Raio relativo da estrela
Luminosidade relativa da estrela
Temperatura da estrela
Luminosidade relativa da estrela